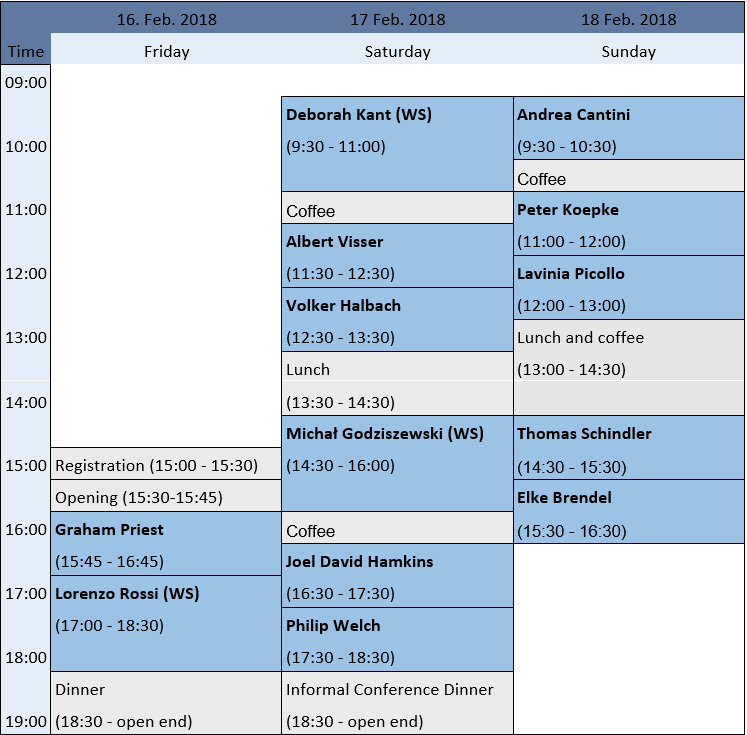
Schedule
Titles and Abstracts
Elke Brendel, Truthmaker Maximalism and the Truthmaker-Paradox
Truthmaker maximalism (TMM) is the view that every true sentence has a truthmaker, where a truthmaker of a sentence σ is conceived as an entity whose mere existence necessitates the truth of σ. Peter Milne has attempted to refute TMM via a self-referential sentence M “saying” of itself that it doesn’t have a truthmaker. Milne argues that M turns out to be a true sentence without a truthmaker and thus provides a counterexample to TMM.
In contrast to Milne’s argument, it will be shown that M leads to a provable contradiction no matter how one assesses TMM. M turns out to be a liar-like sentence that gives rise to a Truthmaker-Paradox (TP). TP is an interesting paradox in its own right, but has no significance for the still virulent question of whether TMM is a philosophically plausible account.
In contrast to Milne’s argument, it will be shown that M leads to a provable contradiction no matter how one assesses TMM. M turns out to be a liar-like sentence that gives rise to a Truthmaker-Paradox (TP). TP is an interesting paradox in its own right, but has no significance for the still virulent question of whether TMM is a philosophically plausible account.
Andrea Cantini, From self-reference to unfoundedness
As a starting point, we reconsider the paradoxes of Russell-Zermelo vs. Burali-Forti and Mirimanoff. We then deal with Yablo's paradox by projecting it into different formal frameworks.
In particular we discuss:
(i) a recent attempt to understand structural aspects underlying Yablo's paradox;
(ii) the same paradox in a classical theory of Frege structures and in a theory of stratified truth.
In particular we discuss:
(i) a recent attempt to understand structural aspects underlying Yablo's paradox;
(ii) the same paradox in a classical theory of Frege structures and in a theory of stratified truth.
Michał Godziszewski, On some metalogical properties of Visser - Yablo sequences and potential infinity (workshop)
You can find the abstract here.
Volker Halbach, Self-reference in Arithmetic?
Many sentences in arithmetic that are of metamathematical interest are described as self-referential. In particular, the Gödel sentence is described as a sentence that claims its own unprovability, while the Henkin sentence is described as a sentence claiming its own provability. More recently philosophers have discussed whether Visser-Yablo sentences are self-referential. The notion of self-reference, however, seems blurry in these discussion; in other cases the analysis of self-reference seems just inadequate. The emphasis of the talk will be on the consequences of the analysis of self-reference for formal results in metamathematics.
Joel David Hamkins, Self-reference in computability theory and the universal algorithm
I shall give an elementary account of the universal algorithm, due to Woodin, showing how the capacity for self-reference in arithmetic gives rise to a Turing machine program e, which provably enumerates a finite set of numbers, but which can in principle enumerate any finite set of numbers, when it is run in a suitable model of arithmetic. Furthermore, the algorithm can successively enumerate any desired extension of the sequence, when run in a suitable top-extension of the universe. Thus, the algorithm sheds some light on the debate between free will and determinism, if one should imagine extending the universe into a nonstandard time scale. An analogous result holds in set theory, where Woodin and I have provided a universal locally definable finite set, which can in principle be any finite set, in the right universe, and which can furthermore be successively extended to become any desired finite superset of that set in a suitable top-extension of that universe.
Comments and inquires can be made on the speaker's blog at http://jdh.hamkins.org/self-reference-in-the-universal-algorithm.
Comments and inquires can be made on the speaker's blog at http://jdh.hamkins.org/self-reference-in-the-universal-algorithm.
Deborah Kant, Set theory on both the meta and the object level (workshop)
This introductory talk is based on the observation that we use set theory to argue about set-theoretic theories and their models. Thus, in certain contexts we employ set theory on both the meta and the object level. For example, a model of ZFC can 'talk about itself', and it is possible, in ZFC, to 'talk about ZFC itself'. This situation makes it difficult to clearly delineate the object and the meta levels in set-theoretic discourses. We approach this problem by considering specific examples, and ask the question whether an identification of the meta and the object level in set theory is possible or not.
The "Self" is a multifacetted notion in Psychology and Philosophy, central to human life and society, but also leading into bewildering conundrums. In mathematics, theories like set theory and even number theory allow versions of self-reference which lead to inconsistencies, paradoxes and incompletenesses.
In my talk I shall show that prudent uses of self-reference account for strong principles. Induction, recursion, ordinal numbers and large cardinals involve substantial self-referentiality. I shall in particular consider elementary maps of models of set theory that can be applied to themselves.
In my talk I shall show that prudent uses of self-reference account for strong principles. Induction, recursion, ordinal numbers and large cardinals involve substantial self-referentiality. I shall in particular consider elementary maps of models of set theory that can be applied to themselves.
Lavinia Picollo, Truth, Reference and Disquotation
I first provide intuitively appealing notions of reference, self-reference, and well-foundedness of sentences of the language of first-order Peano arithmetic extended with a truth predicate. They are intended as a tool for studying reference patterns that underlie expressions leading to semantic paradox, and thus to shed light on the debate on whether every paradox formulated in a first-order language involves self-reference or some other vicious reference pattern.
I use proof-theoretic versions of the new notions to formulate sensible restrictions on the acceptable instances of the T-schema, to carry out the disquotationalist project. Since the concept of reference I put forward is proof-theoretic - i.e., it turns to the provability predicate rather than the truth predicate - and, therefore, arithmetically definable, it can be used to provide recursive axiomatizations of truth. I show the resulting systems are $\omega$-consistent and as strong as Tarski's theory of ramified truth iterated up to $\epsilon_0$.
I use proof-theoretic versions of the new notions to formulate sensible restrictions on the acceptable instances of the T-schema, to carry out the disquotationalist project. Since the concept of reference I put forward is proof-theoretic - i.e., it turns to the provability predicate rather than the truth predicate - and, therefore, arithmetically definable, it can be used to provide recursive axiomatizations of truth. I show the resulting systems are $\omega$-consistent and as strong as Tarski's theory of ramified truth iterated up to $\epsilon_0$.
Graham Priest, This sentence is not provable
Gödel’s first Incompleteness Theorem is often phrased as: any (sufficiently strong) axiomatic arithmetic is incomplete. This is inaccurate: what Gödel’s proof shows is that it is either incomplete or inconsistent. Of course, if classical logic is used, then inconsistency implies triviality; so it is natural enough to ignore the inconsistency alternative. However, this is not so if a paraconsistent logic is used. Indeed, it is now known that there are axiomatic arithmetics that are complete, inconsistent, and non-trivial. In this talk, I will explain what these theories a like, and then turn to the question of what one should make of their existence philosophically.
Lorenzo Rossi, A theory of paradoxes, with an application to some variants of Yablo’s and Visser’s paradoxes (workshop)
Naïveté about truth has it that for every sentence φ (of a sufficiently rich language), φ and ‘φ is true’ are in some sense equivalent. Naïveté about truth is known to generate a wide range of semantic paradoxes, including the Liar, the Truth-teller, Curry’s Paradox and many more. In this paper, I will explore the wide range of semantic behaviours displayed by paradoxical sentences, and the resources that are required to evaluate them. I will propose a new semantic theory of paradoxes that distinguishes between four main kinds of paradoxical sentences (Liar-like paradoxes, Truth-teller-like paradoxes, Revenge paradoxes, and Non-well-founded paradoxes), and gives their semantics in one single model. At the same time, the theory offers a simple formal explication of the notions of self-reference, circularity, and well-foundedness. As an application of the proposed theory, I will investigate in more detail the semantics of (versions of) Yablo’s and Visser’s paradoxes. I will argue that some Yablo- and Visser-like paradoxes are circular but well-founded, while others are non-circular but non-well-founded.
Thomas Schindler, A graph-theoretic analysis of the semantic paradoxes
We introduce a framework for a graph-theoretic analysis of the semantic paradoxes. Similar frameworks for infinitary propositional languages have been investigated by Cook (2004, 2014), Rabern, Rabern, and Macauley (2013), and others. Our focus, however, will be on the language of first-order arithmetic augmented with a primitive truth predicate. Using Leitgeb’s (2005) notion of semantic dependence, we assign reference graphs (rfgs) to the sentences of this language and define a notion of paradoxicality in terms of acceptable decorations of rfgs with truth values. It is shown that this notion of paradoxicality coincides with that of Kripke (1975). In order to track down the structural components of an rfg that are responsible for paradoxicality, we show that any decoration can be obtained ina three-stage process: first, the rfg is unfolded into a tree, second, the tree is decorated with truth values (yielding a dependence tree in the sense of Yablo (1982)) and third, the decorated tree is re-collapsed onto the rfg. We show that paradoxicality enters the picture only at stage three. Due to this we can isolate two basic patterns necessary for paradoxicality. Moreover, we conjecture a solution to the characterization problem for dangerous rfgs that amounts to the claim that basically the Liar- and the Yablo-graph are the only paradoxical rfgs. Furthermore, we develop signed rfgs that allow us to distinguish between ‘positive’ and ‘negative’reference and obtain more fine-grained versions of our results for unsigned rfgs.
Albert Visser, Cogwheels of Self-reference
My talk is a prolegomenon to Volker Halbach’s talk. It consists of two parts.
First, I discuss the usual construction of (supposedly) Self-Referential sentences in theories that interpret a modicum of arithmetic. I will briefly digress on the idea of a Gödel-numbering with built-in Self-Reference.
Secondly, I will present the story of Kreisel's and Löb’s discoveries concerning the Henkin sentence. What are the methodogical and philosophical morals to draw from this story? We will have a look at a possible defect of Kreisel’s paper even by its own internal standards. I briefly consider variations like Rosser-style Henkin sentences and $\Sigma^0_1$-truth-tellers.
First, I discuss the usual construction of (supposedly) Self-Referential sentences in theories that interpret a modicum of arithmetic. I will briefly digress on the idea of a Gödel-numbering with built-in Self-Reference.
Secondly, I will present the story of Kreisel's and Löb’s discoveries concerning the Henkin sentence. What are the methodogical and philosophical morals to draw from this story? We will have a look at a possible defect of Kreisel’s paper even by its own internal standards. I briefly consider variations like Rosser-style Henkin sentences and $\Sigma^0_1$-truth-tellers.
Philip Welch, Higher types of recursion: revision theoretic definitions and infinite time turing machines
The connection between the Herzbergerian flavour of the revision theory of circular definitions, and infinite time Turing machines (ITTM's) is now well understood. We study here higher type versions of these, where revisions are allowed to call on oracles that are themselves the result of revisions of this kind. In the ITTM arena, we can use ideas of Kleene of his higher type recursion with ITTM's, instead of ordinary Turing machines, situated on wellfounded trees of subcomputations. We consider how low levels of determinacy in the arithmetic hierarchy can correspond to the halting problem for certain such recursions.